Linear Equations Made Simple

​​​Graphing Linear Equations in one or two variables: 

Graphing linear equations is a visual way to represent the relationship between two variables. A linear graph is a straight line that shows how the value of one variable changes in relation to the other variable.

​

How can Linear equations be graphed?

There are several techniques for graphing linear equations, like

1. Finding the x and y coordinates

2. Using the slope intercept form, and

3. Using the point slope form.

4. Linear equation in one variable

 

​​​1. Plotting the points:

To graph a linear equation, we can find the x and y coordinates for several points and plot them on a graph.

You can choose values of x as 0,1,2; substitute each these x-values into the given equation to find corresponding values of y.

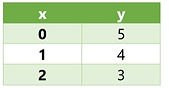
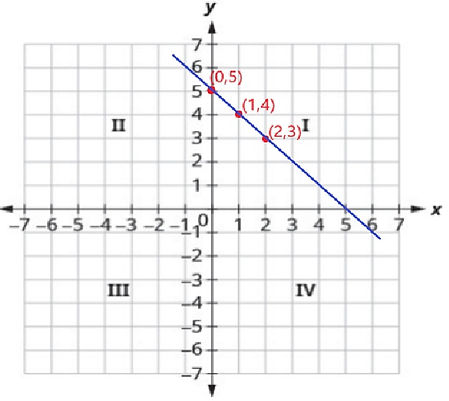
Example: x + y = 5

To graph this linear equation, let's consider x = 0,1,2. 

Step 1: When x = 0

0 + y = 5 (substitute value of x = 0 in the given equation)

y = 5

Point (0, 5) lies on the line x + y = 5 and is the y-intercept

When x = 1, (substitute value of x = 1 in the given equation)

1 + y = 5

y = 4  ( by subtracting 1 on both sides)

Point (1, 4) lies on the line

Lastly x = 2, (substitute value of x = 2 in the given equation)

2 + y = 5

y = 3   (by subtracting 2 on both sides)

Point (2, 3) lies on the line​​​​​

Step 2: Plot the points (0, 5), (1, 4) and (2, 3), join them using ruler.

The line obtained is the graph of the equation x + y = 5

​​2. Graphing a line using its slope-intercept form:

​To plot a line using its slope (m) and y-intercept (b) from an equation

such as y = mx + b, start by marking the y-intercept on the y-axis. 

This point will be (0, y)

Next, apply the slope (rise/run) to determine a second point:

from the y-intercept, move up (or down) by the rise and then

move right (or left) by the run.

Finally, draw a line that connects these points.

Example: y - 1 = 2x

Step 1: 

Convert the given equation in to slope-intercept form

 y = mx + c, where m is the slope and c is the y-intercept

 y – 1 = 2x

 y = 2x + 1 (adding 1 on both sides)

Step 2:

Compare the equation with slope-intercept form

 Slope (m) = 2 and y-intercept = 1

Step 3: Mark a point called y- intercept (0, 1)

(where the line intersects the y-axis with x-coordinate=0) on the graph 

Step 4: Mark another point using the slope

by counting 2 units for the rise and 1 unit for the run

Step 5: Join the two points to get the graph of y-1 = 2x

​

​​3. The x- and y-intercept method:

Find the points where the line crosses the x-axis and the y-axis.

Draw a line through them. 

Example: 3x + 2y = 12

Step 1: Find the x-intercept (a point where the line intersects the x-axis)

Substitute y = 0 in the equation (All points on the x-axis have

y-coordinate = 0)

           3x + 2(0) = 12

            3x = 12

            x = 4

The x-intercept is a point (4, 0)

Step 2: Find the y-intercept (a point where the line intersects the y-axis)

Substitute x = 0 in the equation

(All points on y-axis have x-coordinate = 0)

           3(0) + 2y = 12

            2y = 12

            y = 6

 The y-intercept is a point (0, 6)

Step 3: Plot the x-intercept and y-intercept on the graph and join them

 

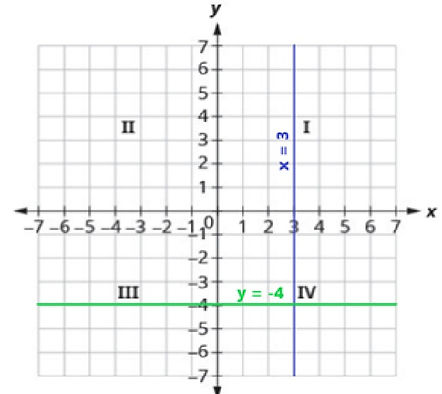
​​​4. Linear equation in one variable:

Graph of a Linear equation in one variable is either parallel

to the x-axis or the y-axis.

Example 1: x = 3

All the points that have their x-coordinate as 3 and have

multiple values of y, lie on the line x = 3

Example 2: y = - 4

All the points that have y-coordinate as -4 and have

multiple values of x, lie on the line y = - 4

​

​

​

​

Solving Linear Equations

A solution to a linear equation is the value of the variable that satisfies the equation and makes the equation true.

​​​​How to solve a linear equation in one variable?

A general strategy for solving linear equations in one variable is simplifying the equation by combining like terms, distributing, and isolating the variable. It is important to check the answer by substituting the solution you found back into the original equation. If the left side of the equation equals the right side, your solution is correct.

Example: 2(x-1) - 2 = 3(2x + 3) + 1

  Step 1: Simplify each side of equation Using distributive property

               2x - 2 - 2 = 6x + 9 + 1

               2x - 4 = 6x + 10

  Step 2: isolating the variables by subtracting 6x on both sides and adding 4 on both sides.

              2x - 4 - 6x + 4 = 6x + 10 - 6x + 4

  Step 3: Combining like terms

              -4x = 14

                x = - 14/4                      (Dividing by -4 on both sides)

                x = -7/2

​

You can use an algebra calculator to solve linear equations and a graphing calculator to graph linear equations.

​

What is the solution for the system of linear equations?

The solution for a system of linear equations is the set of values for the variables that satisfy all the equations in the system simultaneously. There are three possible types of solutions for a system of linear equations:

1. Unique Solution: The system has a single solution (a point) where the lines intersect at a single point and all the variables take specific values that satisfy all the equations.

Note:  A unique solution can be found if the number of equations is equal to the number of variables.

2. No Solution: The system has no solution when the equations are inconsistent, meaning they represent parallel lines or planes that do not intersect.

3. Infinite Solutions: The system has infinitely many solutions when the equations are dependent and represent overlapping lines or planes. In this case, the variables can take any values that satisfy the equations.

 

What are the techniques for solving system of two linear equations in two variables?

To solve a system of two linear equations in two variables, various techniques can be used, including elimination, substitution, matrix operations and graphing.

1. Solving system of Linear Equations by Elimination:

This is an algebraic method that involves adding or subtracting the two equations to cancel out or "eliminate" one of the variables. 

Example: 4x + 3y = 11

2x - y = 3

Step 1: To eliminate one of the variables, add or subtract the equations. In this case let’s eliminate “x”. For this we need to multiply equation 2 by “2” to make the coefficients of x equal. Then the equation 2 becomes 4x-2y = 6

4x + 3y = 11       (Eq. 1)

4x - 2y = 6             (Eq. 2)

Step 2: Subtract eq. 2 from 1

(4x + 3y) – (4x - 2y) = 11 - 6

4x + 3y - 4x + 2y =5

5y = 5

y = 1

Step 3: Substitute this value of y into either Equation 1 or Equation 2

2x - 1 = 3    (adding 1 on both sides)

Step 4: Simplifying the equation

2x = 4  (Dividing by 2 on both sides)

x = 2

Hence, x=2, y=1 is the solution to the given system of linear equations.

​

2. Solving system of Linear Equations by Substitution:

In this method we isolate one variable in one equation and then substitute that expression into the other equation. 

Example: 2x - 3y = 10      ( equation 1)

                x+ y = 6            ( equation 2)

Step 1: Solve one equation for one variable. In this case let’s solve equation 2 for the value of x.

x = 6 - y

Step 2: Substitute it into the other equation 1 (in this case)

2(6 - y) – 3y = 10

Step 3: Expanding and simplifying the equation:

12 – 2y – 3y = 10

12 - 5y = 10

- 5y = 10 - 12         (Subtracting 12 on both sides)

- 5y = - 2                  ( Divide by - 5 on both sides)

y = 2/5  

x = 6 -  (2/5)      (Substitute value of y in equation 2)

x = 28/5

​​

Solving system of Linear Equations by Graphing:

To solve the system of equations using the graphing method, plot given linear equations on a coordinate plane.

The point where the two lines intersect is the solution of the given linear equations.

Example: 3x + 2y = 12 -------1

                  2x – y = 1 ------- 2

Step 1:

Convert both the equations in the slope-intercept form

3x + 2y = 12

2y = – 3x + 12 (Subtract 3x from both sides)

y =  x + 6 (Divide 2 on both sides) ------1

2x - y = 1

– y = – 2x + 1 (Subtract 2x on both sides)

y = 2x – 1 (Multiply -1 on both sides) ------2

Step 2:

Identify the slope and y-intercept of equations 1 and 2

Equation 1: slope = -3/2, y-intercept = 6

Equation 2: slope = ,2, y-intercept = – 1

Step 3:

Graph equation 1

Mark the point y-intercept A (0, 6)

Mark another point B (-3, 8) (Start from (0, 6), move 3 units down and 2 units right) using slope -3/2)

Join AB

Step 4:

Graph equation 2 on the same coordinate plane

Mark the point y-intercept P (0, -1)

Mark another point Q (1, 1)) (Start from (0, -1), move 2 units up and 1 unit right) using slope 2)

Join PQ

Step 5:

Identify the point where two lines intersect:

The point of intersection of two lines B (2, 3) is the solution to given system of equations.

​

 Why is it important for students to learn about Linear Equations?

 The importance of mastering linear equations is that they are a fundamental concept in mathematics and mastering them is crucial for success in high school math courses like Algebra 1, Algebra 2, Geometry, and Trigonometry. Additionally, understanding linear equations is essential for problem-solving in various fields, from calculating the cost of goods to designing a bridge. They are also essential in fields such as engineering, economics, and science. 

​

​​​Solve Linear Equations worksheets >>